Class 10 Polynomials Previous Year Questions
Q1:
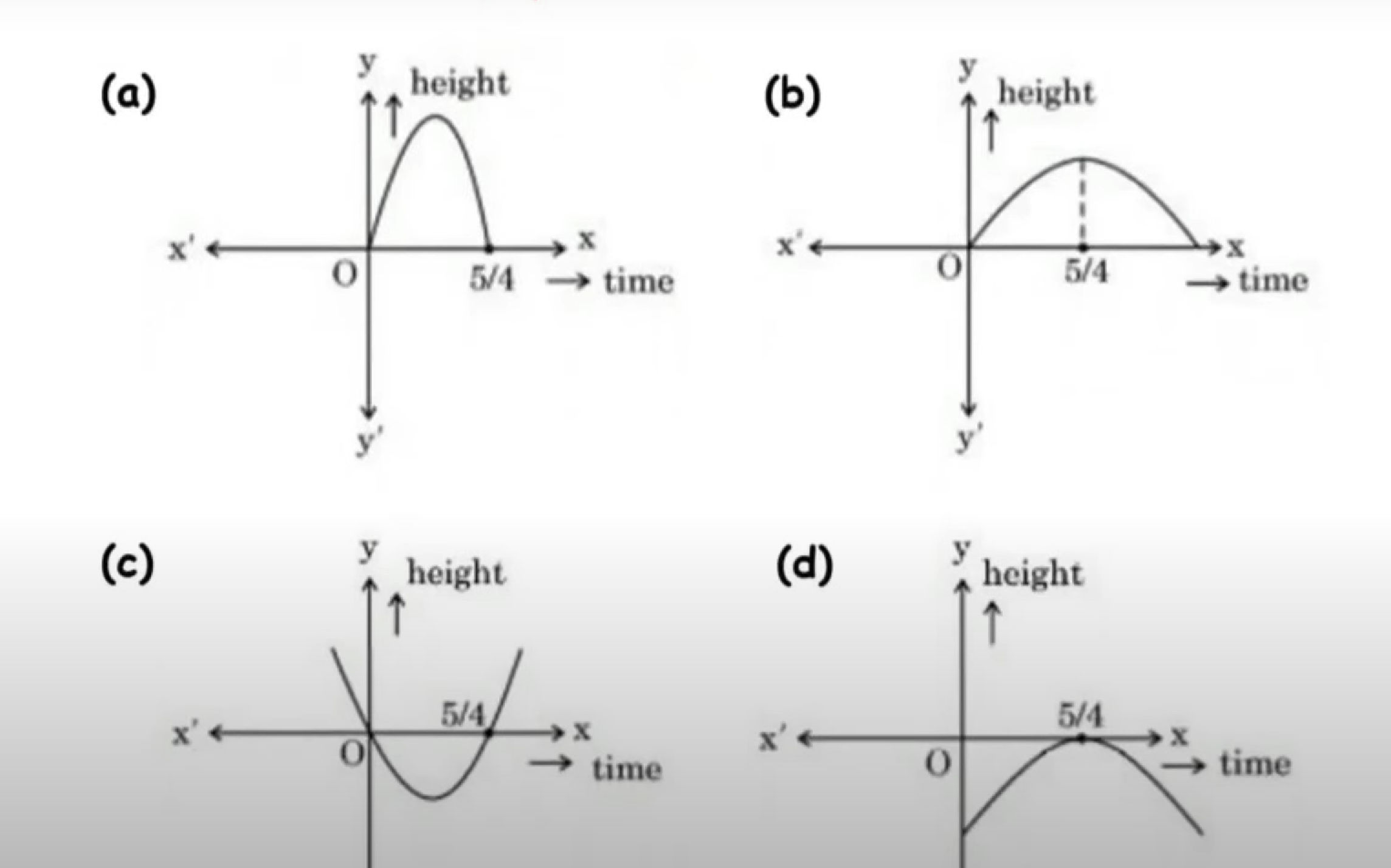
Two polynomials are shown in the graph below. The number of distinct zeroes of both the polynomials is : (A) 3 (B) 5 (C) 2 (D) 4
CBSE [2025]
HardQ2:
If \(\alpha\) and \(\beta\) are the zeroes of the polynomial \(p(y) = y^2 - 5y + 3\), then find the value of \(\alpha^4\beta^3 + \alpha^3\beta^4\)
CBSE [2025]
EasyQ3:
Zeroes of the polynomial \(p(x) = x^2 - 3\sqrt{2}x + 4\) are :
CBSE [2025]
EasyQ4:
If \(\alpha\) and \(\beta\) are the zeroes of the polynomial \(p(x) = x^2 - ax - b\), then the value of \(\alpha + \beta + \alpha\beta\) is equal to :
CBSE [2025]
EasyQ5:
If p and q are zeroes of the polynomial \(p(y) = 21y^2 - y - 2\), then find the value of (1 - p)(1 - q)
CBSE [2025]
EasyQ6:
Find the zeroes of the polynomial p(x) = \(x^2 + \frac{4}{3}x - \frac{4}{3}\)
CBSE [2025]
EasyQ7:
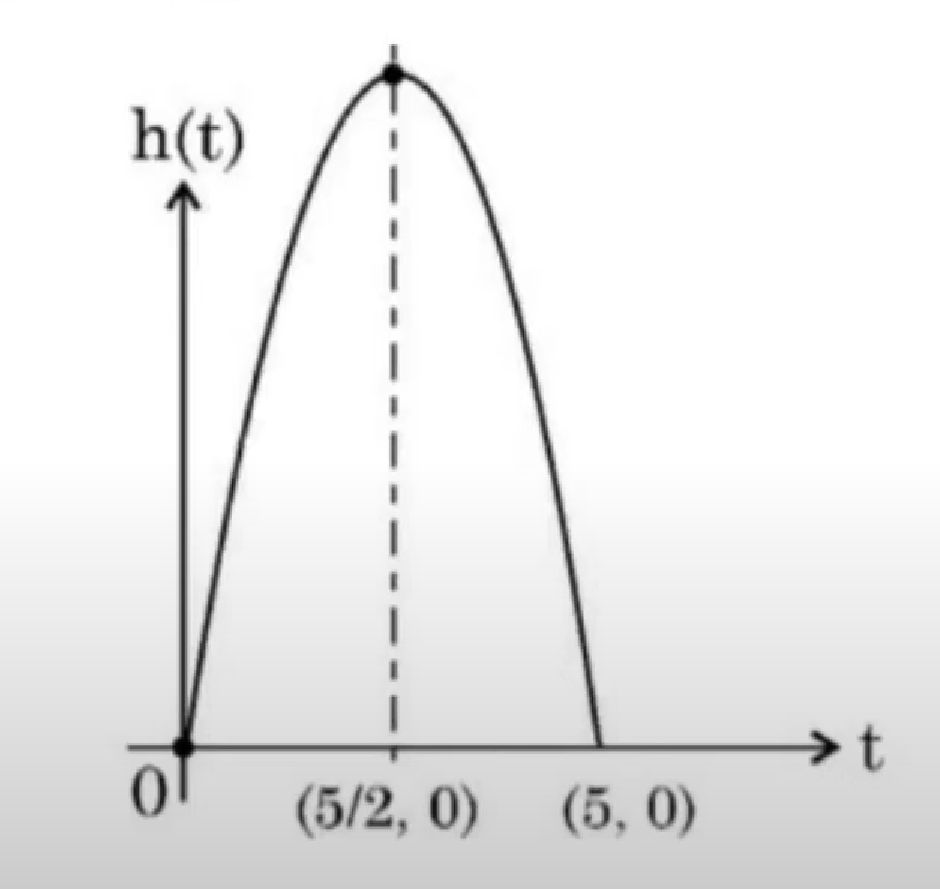
A ball is thrown in the air so that t seconds after it is throw, its height h metre above its starting point is given by the polynomial h = 25t - 5t². Observe the graph of the polynomial and answer the following questions: (i) Write zeroes of the given polynomial. (ii) Find the maximum height achieved by the ball. (iii) (a) After throwing upward, how much time did the ball take to reach to the height of 30m? OR (b) Find the two different values of t when the height of the ball was 20m.
CBSE [2024]
MediumQ8:
If α and β are zeroes of the polynomial 5x² + 3x - 7, find the value of \(\frac{1}{α} \) + \(\frac{1}{β} \).
CBSE [2024]
EasyQ9:
The zeroes of a polynomial x² + px + q are twice the zeroes of the polynomial 4x² - 5x - 6. Then find the value of p.
CBSE [2024]
EasyQ10:
If the sum of zeroes of the polynomial p(x) = 2x² - k\( \sqrt{2} \)x + 1 is \( \sqrt{2} \), then the value of k is:
CBSE [2024]
EasyQ11:
Which of the following quadratic equations has sum of its roots as 4 ? (a) 2x² - 4x + 8 = 0 (b) -x² + 4x + 4 = 0 (c) \( \sqrt{2} \)x² - \(\frac{4}{√2x + 1} \) = 0 (d) 4x² - 4x + 4 = 0
CBSE [2023]
EasyQ12:
If one zero of the polynomial 6x² + 37x – (k – 2) is reciprocal of the other, then find the value of k.
CBSE [2023]
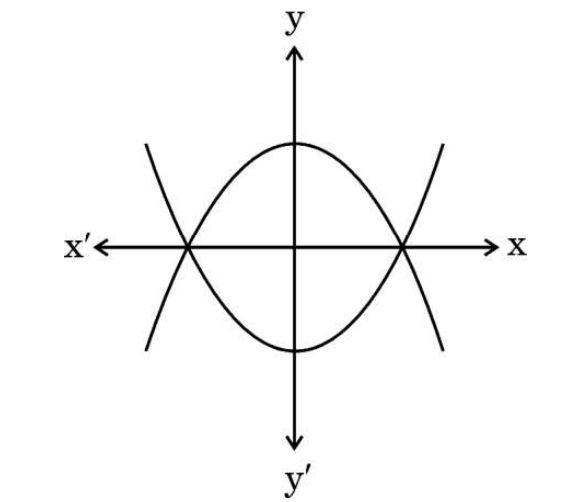
EasyQ13:
In a pool at an aquarium, a dolphin jumps out of the water travelling at 20 cm per second. Its height above water level after t seconds is given by h = 20t - 16t². Based on the above, answer the following questions: (i) Find the zeroes of the polynomial p(t) = 20t - 16t² (ii) (a) What would be the value of h at t = \(\frac{3}{2}\)? Interpret the result. OR (b) How much distance has the dolphin covered before hitting the water level again? (iii) Which of the following types of graph represents p(t) ?