Class 10 Quadratic Equations Previous Year Questions
Q1:
The time taken by a person to travel an upward distance of 150 km was 2\(\frac{1}{2}\) hours more than the time taken in the downward return journey. If he returned at a speed of 10 km/h more than the speed while going up, find the speeds in each direction.
CBSE [2025]
HardQ2:
The sum of the areas of two squares is 52 \(cm^2\) and difference of their perimeters is 8 cm. Find the lengths of the sides of the two squares.
CBSE [2025]
MediumQ3:
The age of a man is twice the square of the age of his son. Eight years hence, the age of the man will be 4 years more than three times the age of his son. Find their present ages.
CBSE [2024]
MediumQ4:
Find the value of 'c' for which the quadratic equation (c + 1)x² - 6(c + 1)x + 3(c + 9) = 0, where c ≠ -1, has real and equal roots.
CBSE [2024]
HardQ5:
A train travels a distance of 90 km at a constant speed. Had the speed been 15 km/h more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
CBSE [2024]
HardQ6:
The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2 16/21, find the fraction.
CBSE [2024]
MediumQ7:
In a flight of 2800 km, an aircraft was slowed down due to bad weather. Its average speed is reduced by 100 km/h and by doing so, the time of flight is increased by 30 minutes. Find the original duration of flight.
CBSE [2024]
HardQ8:

A rectangular floor area can be completely tiles with 200 square tiles. If the side length of each tile is increased by 1 unit, it would take only 128 tiles to cover the floor. (i) Assuming the original length of each side of a tile be x units, make a quadratic equation from the above information. (ii) Write the corresponding quadratic equation in standard form. (iii) (a) Find the value of x, the length of side a tile by factorisation. OR (b) Solve the quadratic equation for x, using quadratic formula.
CBSE [2024]
MediumQ9:
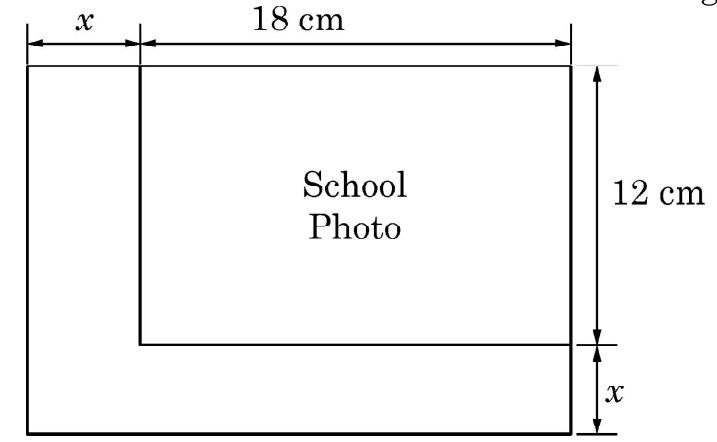
While designing the school year book, a teacher asked the student that the length and width of a particular photo is increased by x units each to double the area of the photo. The original photo is 18 cm long and 12 cm wide. Based on the above information, answer the following questions: (i) Write an algebric equation depicting the above information. (ii) Write the corresponding quadratic equation in standard form. (iii) (a) What should be the new dimensions of the enlarged photo ? OR (b) (iii) Can any rational value of x make the new area equal to 220 cm² ?
CBSE [2023]
MediumQ10:
Find the value of ‘p’ for which the quadratic equation px(x – 2) + 6 = 0 has two equal real roots.
CBSE [2023]
MediumQ11:
Two pipes together can fill a tank in \(\frac{15}{8}\) hours. The pipe with larger diameter takes 2 hours less than the pipe with smaller diameter to fill the tank separately. Find the time in which each pipe can fill the tank separately.
CBSE [2023]
HardQ12:
A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the journey, what was its first average speed?
CBSE [2023]
HardQ13:
